En numerosas ocasiones hemos citado como valor general de reactancia aceptable para conductores 0,08 Ω/km según la norma francesa UTE C 15-105. En el siguiente artículo procedemos a demostrar el porqué de este valor generalizado así como las fórmulas para el cálculo de la reactancia inductiva de los conductores
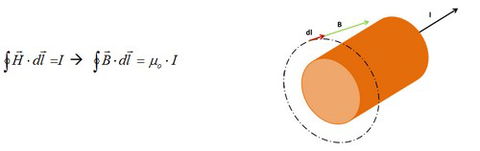
Cuando por un conductor circula una corriente eléctrica variable, se crea en su entorno un campo magnético también variable que rodea tanto al propio conductor que lo genera como al resto de conductores del circuito al que pertenecen.
La energía almacenada por unidad de longitud en el campo magnético que rodea a una línea monofásica en el espacio que la separa de la línea de retorno tiene la siguiente expresión:
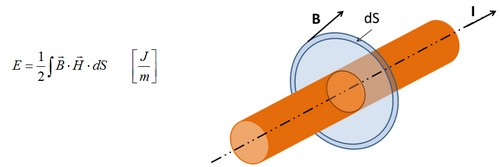
Donde:
B: Inducción magnética o campo magnético B
H: Intensidad de campo magnético o campo magnético H
dS: Elemento de superficie transversal que rodea el eje de nuestra línea
Si tenemos en cuenta que el cociente entre la inducción (B) y la intensidad de campo magnético (H) es la permeabilidad magnética (µo) para materiales no dispersivos:
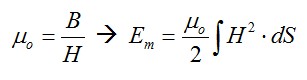
Según la ley de Ampere, la circulación del vector intensidad de campo magnético (H) a lo largo de una línea cerrada es igual a la suma algebraica de las intensidades de corriente que atraviesan la superficie limitada por esa línea cerrada.
Aplicado al caso de un conductor eléctrico en el entorno que lo separa de la línea de retorno:
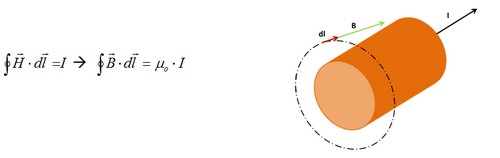
El primer término de la ecuación se convierte en (supuestos valores eficaces constantes de intensidad y por tanto del campo magnético creado):
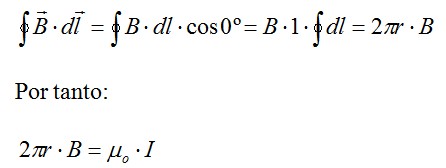
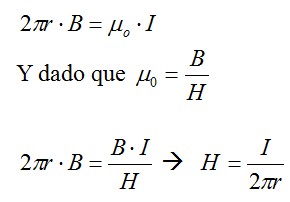
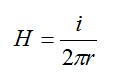
Dentro del conductor (r < R) considerando corriente uniformemente distribuida por tratarse de corriente senoidal a frecuencia industrial que es baja y por tanto el efecto piel no es muy acusado:
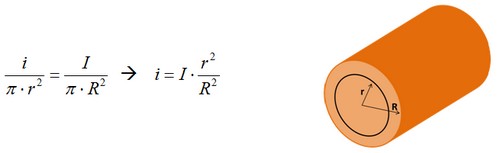
Con lo que la intensidad de campo magnético en el interior del conductor será:
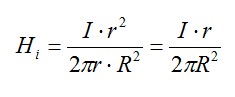
En el exterior sabemos que vale:
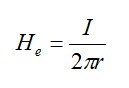
Sumando la energía magnética por unidad de longitud interior (r ≤ R) y exterior (r > R) obtendremos el total de la energía almacenada en el campo magnético que rodea al cable tomando como límite para el cálculo de la energía magnética (Em) el conductor de retorno:
Como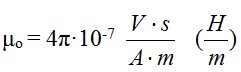 
(se considera que el conductor es un medio no magnético, lineal e isótropo de ahí considerar este valor de permeabilidad magnética).
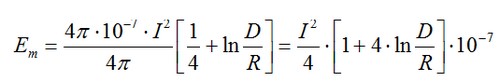
Y dado que sabemos que la energía almacenada en forma de campo magnético por inducción magnética se obtiene a partir de la expresión que relaciona la tensión con la intensidad en una bobina o autoinducción:
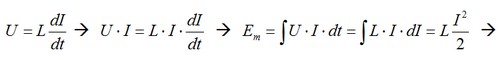
H (henrio): unidad de inductancia eléctrica (L). Es la inductancia eléctrica de un circuito cerrado en el que se produce una fuerza electromotriz de un voltio, cuando la corriente eléctrica que recorre el circuito varía uniformemente a razón de un amperio por segundo.
Obtendremos las expresiones del punto 6, apartado K del catálogo Prysmian de cables y accesorios para BT poniendo la expresión en logaritmo decimal (multiplicando por 2,3) y en H/km.
En caso de tratarse de línea trifásica podremos considerar que la inductancia es el valor medio de la suma de las inductancias debidas a cada par de conductores considerando cada distancia entre dos conductores Dij. Por lo que partiendo de la expresión anterior obtenemos para cada conductor:
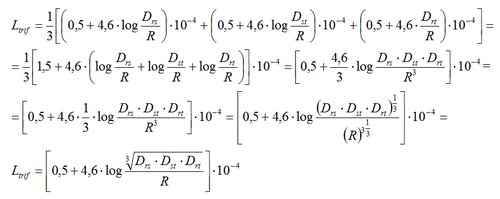
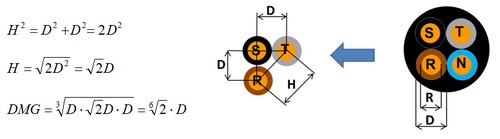
En este caso de más de 2 conductores en lugar de D (distancia entre conductores) observese que debemos aplicar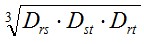 
que se conoce como distancia media geométrica (DMG) Para tres conductores al tresbolillo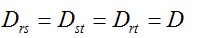 
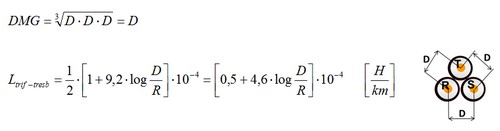
Y para el caso de una línea trifásica con los conductores en un plano:
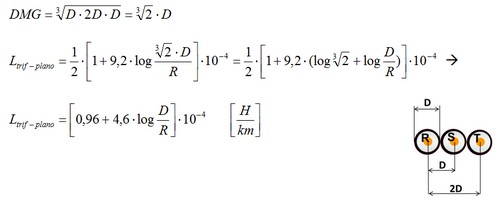
Ejemplo 1
Cálculo de la reactancia inductiva en una red trifásica formada por cables unipolares de cobre de 1x240 mm² Afumex Easy (AS) (RZ1-K (AS)) colocados a tresbolillo:
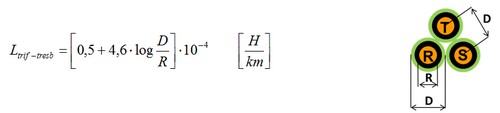
En el catálogo Prysmian de cables y accesorios para BT podemos encontrar los valores de R y D:
R = 24/2 = 12 mm (pág. 103, versión 2014-2015)
D = 26,9 mm (pag. 157 versión 2014-2015)
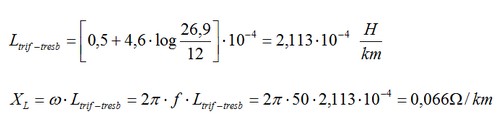
Ejemplo 2
Línea monofásica con conductores de cobre Afumex Plus (AS) (H07Z1-K TYPE 2 (AS)) de 1x16 mm²
Ejemplo 3
Línea trifásica con conductores de aluminio Al Voltalene Flamex (S) (AL XZ1 (S)) de 1x50 mm² situados en un plano.
Ejemplo 4
Línea trifásica con cable Retenax Flex (RV-K) 4X95 mm² (conductores de cobre)
R = 15,1/2 = 7,55 mm (pág. 103)
D = 2 x 1,1 + 15,1 = 17,3 mm (pág. 188) (2 veces 1,1 porque en la tabla figura el espesor de aislamiento)
Podemos afinar el cálculo empleando la distancia media geométrica entre los conductores que corresponde:
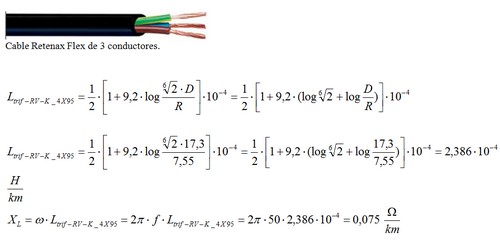
Ejemplo 5
Línea trifásica con conductores Al Afumex (AS) (AL RZ1 (AS)) de 1x150 mm² colocados en un plano.
Observamos que en líneas generales el valor de la reactancia por unidad de longitud no difiere mucho del valor 0,08 Ω/km de la aproximación general para conductores en contacto de la norma francesa UTE C 15-105.
Los valores de reactancia son necesarios para los cálculos de cortocircuito y para los cálculos de caída de tensión cuyas fórmulas figuran en la página 50 del citado catálogo Prysmian de cables y accesorios para BT y que reproducimos a continuación:
(El valor de x en la fórmula para sistemas monofásicos es por km de conductor y no de línea). El peso de la reactancia en la caída de tensión se puede considerar despreciable para conductores de cobre de menos de 35 mm² o conductores de aluminio de menos de 70 mm², en ese caso en las fórmulas anteriores para obtención de la sección por caída de tensión x sería igual a cero lo que simplificaría mucho los cálculos. Por último recordar que para cálculos con corriente continua constante las reactancias no entran en juego al no haber inducciones por no producirse variación del campo magnético asociado a la corriente eléctrica (al no variar la corriente en el tiempo no varía el campo magnético asociado).
La caída de tensión se obtendría con la misma fórmula para sistemas monofásicos con x=0 y cosϕ=1 (este valor del coseno de ϕ es totalmente coherente con la ausencia de reactancia en la línea -->senϕ=0 --> x=0).