Cuando el resultado de un cálculo de sección de conductor es tal que supera la sección máxima disponible en stock lo habitual es emplear varios conductores por fase. Al igual que cuando se emplea un conductor por fase no es difícil obtener las pérdidas por efecto Joule.
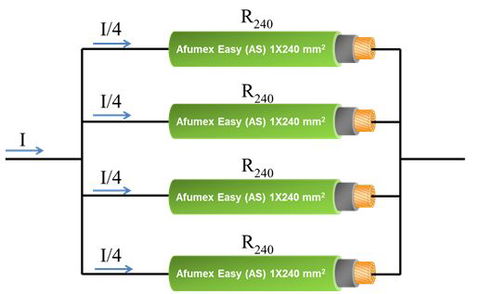
Imaginemos una línea trifásica de 128 m que debe transportar 1200 A y que tras hacer los cálculos oportunos nos resulta que debemos emplear 4 conductores de 1X240 mm² de cobre Afumex Easy (AS) (RZ1-K (AS)) por fase.

Sabemos que las pérdidas térmicas por efecto Joule responden a la expresión:
Ep = n·R·I²·t
Donde n es el número de conductores cargados en la línea (2 para monofásica o continua y 3 para trifásica), R es la resistencia en ohmios (0,106 Ω/km para un conductor de cobre de 1X240, a 90 ºC), I la corriente en amperios (1200 A) y t el tiempo en horas (supongamos un mes = 30 x 24 = 720 h) para obtener la energía perdida (Ep) en Wh.
Puede surgir la duda a la hora de pensar en el valor de resistencia o de intensidad a aplicar para obtener el resultado. Razonémoslo de dos maneras distintas comprobando que los números son iguales.
1.- Supongamos que toda la intensidad I recorre la asociación de resistencias de conductor en paralelo.
Sabemos que la asociación de resistencias en paralelo obedece a la siguiente expresión:
1/RT = 1/R1 + 1/R2 + ... + 1/Rn
Para nuestro caso de 4 conductores por fase, correctamente ordenados y de igual Ri, tenemos:
1/RT = 1/R240 + 1/R240 + 1/R240 + 1/R240 = 4/R240 ➜ RT = R240/4

Línea equivalente por fase
R240 en nuestro caso es igual a:
R240 = 0,106 Ω/km x 0,128 km = 0,013568 Ω
RT = R240/4 = 0,013568/4 = 0,003392 Ω
Por RT pasa toda la intensidad I (1200 A), por lo que las pérdidas por efecto Joule en un mes serán:
Ep1 = n · RT · I2 · t = 3 x 0,003392 x 12002 x 720 = 10 550 476,8 Wh ≈ 10550 kWh
2.- Esta segunda demostración es más evidente. Supongamos que consideramos la intensidad de línea, que es la que circula por una fase. Estará dividida por igual y repartida por cada uno de los cables de 1X240 mm² de esa fase, que tienen su resistencia R240 = 0,106 Ω/km x 0,128 km = 0,013568 Ω.
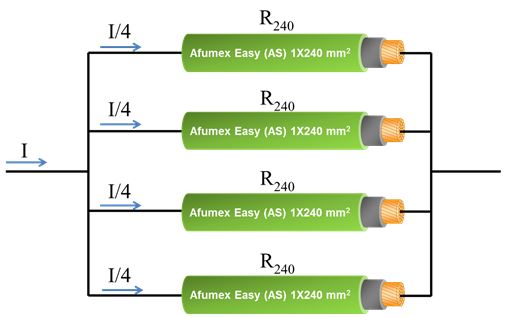
Línea por fase
Bajo este supuesto, al haber 4 conductores por fase, cada uno llevará una corriente I/4 y la aplicación de la fórmula de pérdidas por efecto Joule resultará:
Ep2 = n · 4 · R240 · (I/4)2 · t = 3 x 4 x 0,013568 x (1200/4)2 x 720 = 10 550 476,8 ≈ 10550 kWh
Comprobamos que con ambos procedimientos el resultado es idéntico.
Ocurre que suele costar más imaginar que una resistencia equivalente de un conjunto de resistencias mayores en paralelo pueda consumir lo mismo que estas resistencias por separado a lo que se añade la influencia matemática del cuadrado de la intensidad de corriente para romper esquemas mentales.
Ep1 = n · RT · I2 · t à al ser trifásica y RT = R240/4 à Ep1 = 3 · R240/4 · I2 · t = 3/4 · R240 · I2 · t
Ep2 = n · 4 · R240 · (I/4)2 · t = 3/4 · R240 · I2 · t ➜
Ep1 = Ep2
Con carácter general se puede concluir que la energía térmica perdida en una línea de uno o varios conductores por fase responde a la siguiente expresión:
Ep = n/c ·R · I² · t
Dónde:
- Ep = energía perdida en la línea por efecto Joule (Wh)
- n = 2 para monofásica o continua y 3 para trifásica
- c = número de conductores por fase (1, 2, 3, 4, 5...)
- R = resistencia de cada uno de los conductores activos (es decir, cualquier conductor que no sea de protección o de neutro en trifásica equilibrada y esencialmente libre de armónicos) (Ω)
- I = intensidad de corriente de línea (A)
- t = tiempo (h)
Incrementos de sección para ahorrar pérdidas
En el ejemplo hemos podido ver que las pérdidas térmicas son elevadas. Es verdad que se ha considerado una corriente elevada y constante en el tiempo, pero sirvan estos números sencillos para reflexionar en el sentido de pensar en la reducción de la resistencia de los conductores instalando secciones superiores a las obtenidas por criterios técnicos (o aumentando el número de conductores por fase como procedería en el ejemplo desarrollado en el caso desarrollado). La amortización económica del mayor desembolso inicial en cable (y otros elementos eléctricos) puede ser muy corta y además estaremos contribuyendo a la reducción de emisiones de CO2 al reducir la generación energía.
Si por ejemplo hubiéramos pensado en instalar un conductor más por fase podemos ver cual sería el ahorro de energía fácilmente:
Ep = 3/4·R240 · I² · t – 3/5·R · I² · t = 3/20·R240 · I² · t = 3/20 x 0,013568 x 1200² x 720 = 2 110 095,36 Wh ≈ 2110 kWh
Vemos que la sección total se ha multiplicado por 1,25 al añadir un 25 % más de sección a cada fase y sus pérdidas se han reducido en factor (1-1/1,25) = 0,8 à (1-0,8)·Ep = 0,2 x 10550 kWh = 2110 kWh
Con carácter general vemos que el ahorro de energía perdida por incremento de sección en un conductor por fase sería:
Epahorr = EpS - EpS+1 = n/c ·R · I² · t - n/(c+1) ·R · I² · t = n/(c·(c+1)) ·R · I² · t
Autor:
Lisardo Recio Maíllo
Product Manager de Prysmian Group
Descarga el catálogo Prysmian de Cables y Accesorios para BT
